Štylizácia zrkadlového odlesku
Pridaný: 2014-12-13 17:59:54 (Upravené: 2014-12-14 07:29:12) (Prečítané: 264)
Lesklé plôšky na objekte nám nielen zvýrazňujú najjasnejšie oblasti na povrchu objektu, ale aj zdôrazňujú rôzne materiálové vlastnosti ako napríklad drsnosť, mäkkosť, kovový alebo plastický vzhľad. Budeme tvoriť fragment shader, pomocou ktorého sa budeme snažiť dosiahnúť rôzné zrkadlové odlesky.
Vo fragment shadery budeme kontrolovať, či skalárny súčin, (H, L) > 1 - ε, kde ε je užívateľsky definovaná miera šírky lesku.
Pre polovičný vektor H platí,
H:= (L + V)/ ||L + V||, kde
L je svetelným vektorom a V je vektor pohľadu a N je normála plôšky.
Obrys lesku
Aby sa efekt komixovej ilustrácie ešte viac zdôraznil, vytvoríme obrysy okolo lesku, čo znamená, že vytvoríme čiernu linku na vonkajšej hranici oblasti lesku. Pozri Obr.1. Obrys lesku sa vytvorí na miestach, kde platí, že H,
(H, N) > (1- ε) - ε / 10 a sú to obrazové body na hranici lesku vyznačené čiernou farbou.
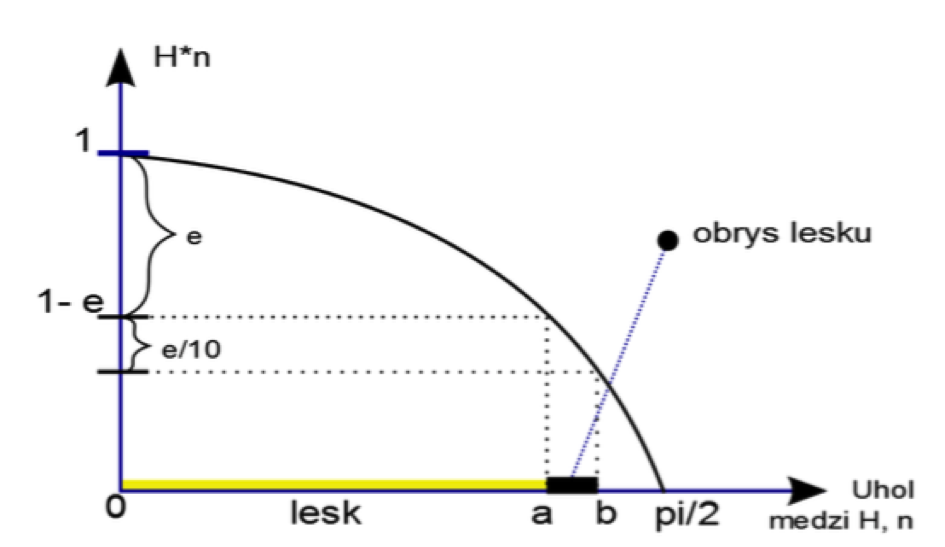
Na (Obr.1) je znázornený graf funkcie, ktorý pozostáva z vodorovnej súradnicovej osi, vyjadrujúcej veľkosť uhla medzi H a N a zvislej osi vyjadrujúcej hodnotu skalárneho súčinu (H, N). Vektory H, ktoré tvoria lesk, zvierajú s vektorom N uhol v intervale (0, a) a vektory H, ktoré tvoria okraj lesku, zvierajú uhol s vektorom N v intervale (a, b).
Nasledovný kód ukazuje spôsob výpočtu lesku a jeho obrysu vo fragment shadery. Bodom s prislúchajúcim vektorom H, tvoriacich lesk, podľa (Obr.1), sme jednoducho priradili bielu farbu. Bodom s prislúchajúcim vektorom H, patriacich do obrysu lesku, podľa (Obr.1), sme priradili čiernu farbu.
float e = 0.01;
if (dot(H,n) > (1 - e - e * 0.1))
{
//--cierny obrys lesku--//
color = vec4 (0, 0, 0, 0);
if (dot(H,n) > (1 - e))
//--biely lesk--//
color = vec4 (1, 1, 1, 0);
}
gl_FragColor = color;
Výhodou fragment shaderu je, že pri vykresľovaní obrysu objektu, nám umožní vykresliť nielen úplné obrysy objektu, ale aj vnútorné obrysy vo vnútri objektu. Pri vykresľovaní sa hrúbka obrysu rôzne mení, ako môžeme pozorovať aj na (Obr.1).

Rozdelenie lesku
V komixoch sa často používa rozdelenie leskov na viacero častí, aby zvýraznili odraz okolitého prostredia. V nasledujúcej časti budeme popisovať metódu, ako sme rozdelili náš lesk na štyri časti, aby sme simulovali odraz štyroch častí okien.

Na (Obr.3) je objekt s jedným leskom na ľavej strane, v strede je objekt s leskom rozdelený na dve časti a vpravo je objekt s leskom rozdelený na štyri časti. Rozdelenie lesku prebehne tak, že pôvodný lesk rozdelíme na štyri kvadranty a každý bod lesku skopírujeme do štyroch rôznych kvadrantov.
V prvom kroku musíme jednoznačne definovať súradnice vektora H, pomocou smerových kosínusov, (H_u, H_v, H_n), v lokálnom súradnicovom systéme, prislúchajúce danému bodu povrchu, (d_u, d_v, N), kde d_u a d_v je dotyčnica a vedľajšia dotyčnica k ploche a N je normála k ploche, pozri (Obr.4). Každý vektor H, patriaci do lesku posunieme o hodnotu φ a ψ, v smere d_u a d_v, podľa toho, v ktorom kvadrante H leží. Súradnice posunutého vektora f_p(H) sú presnejšie dané týmto vzťahom,
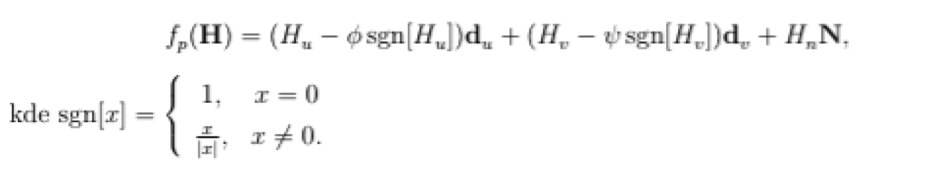
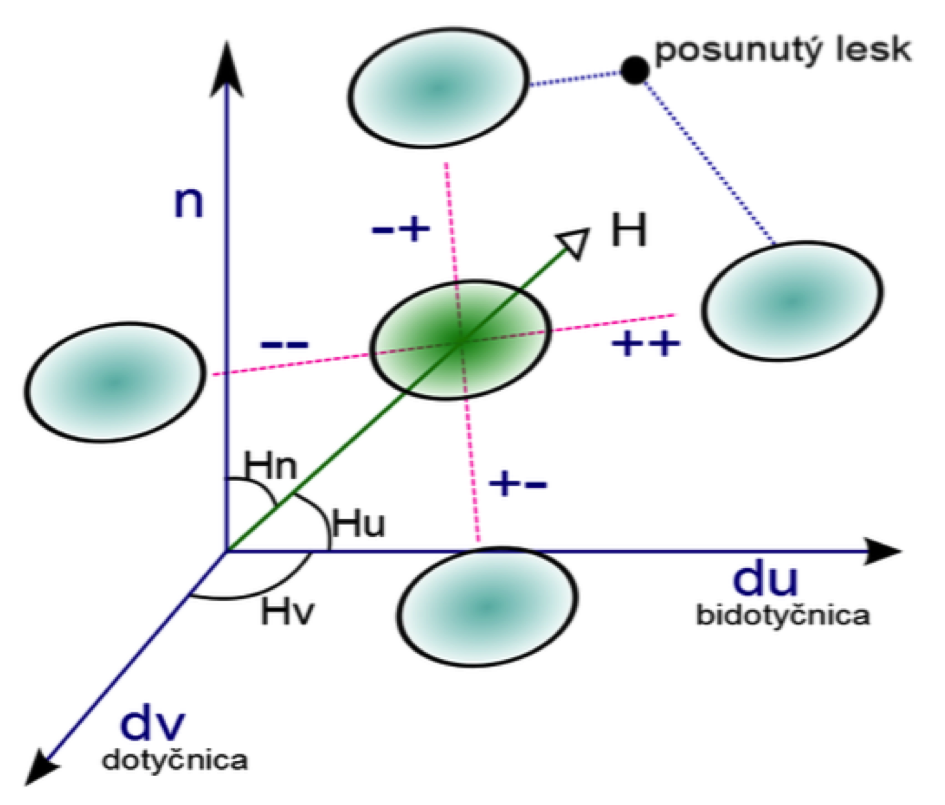
Nasledujúca časť programu počíta lokálny súradnicový systém, vzhľadom na dotyčnice d_u, vedľajšie dotyčnice d_v a normály N, zo svetelného vektora. Ďalej sa rátajú smerové kosínusy (H_u, H_v, H_n). Posunutie je na začiatku dané φ = 0.2 a ψ = 0.1 a je voliteľné užívateľom. V kóde nasleduje výpočet nových súradníc posunutého vektora, H a nakoniec rátame veľkosť lesku pre novovypočítaný vektor ako skalárny súčin (H, N)^1000.
vec3 bitangent = normalize( cross(lightDir, n));
vec3 tangent = normalize( cross (n, bitangent));
float Hu = dot(H, bitangent);
float Hn = dot(H, n);
float Hv = dot(H, tangent);
float phi = 0.2;
float psi = 0.1;
Hu -= phi * sign(Hu);
Hv -= psi * sign(Hv);
float HdotN = normalize(vec3(Hu, Hn, Hv)).y;
vec4 spec_col = pow(HdotN, 1000)* vec4(1,1,1,0);